7.5 angular momentu(角动量)_哔哩哔哩_bilibili
6.4Energy in Rotation Motion
有质量有速度的物体有动能,是不是很有道理

international system(from French systeme international,acronym,SI)of ineria kg*m^2

转动动能:物体由于运动所具有的能量
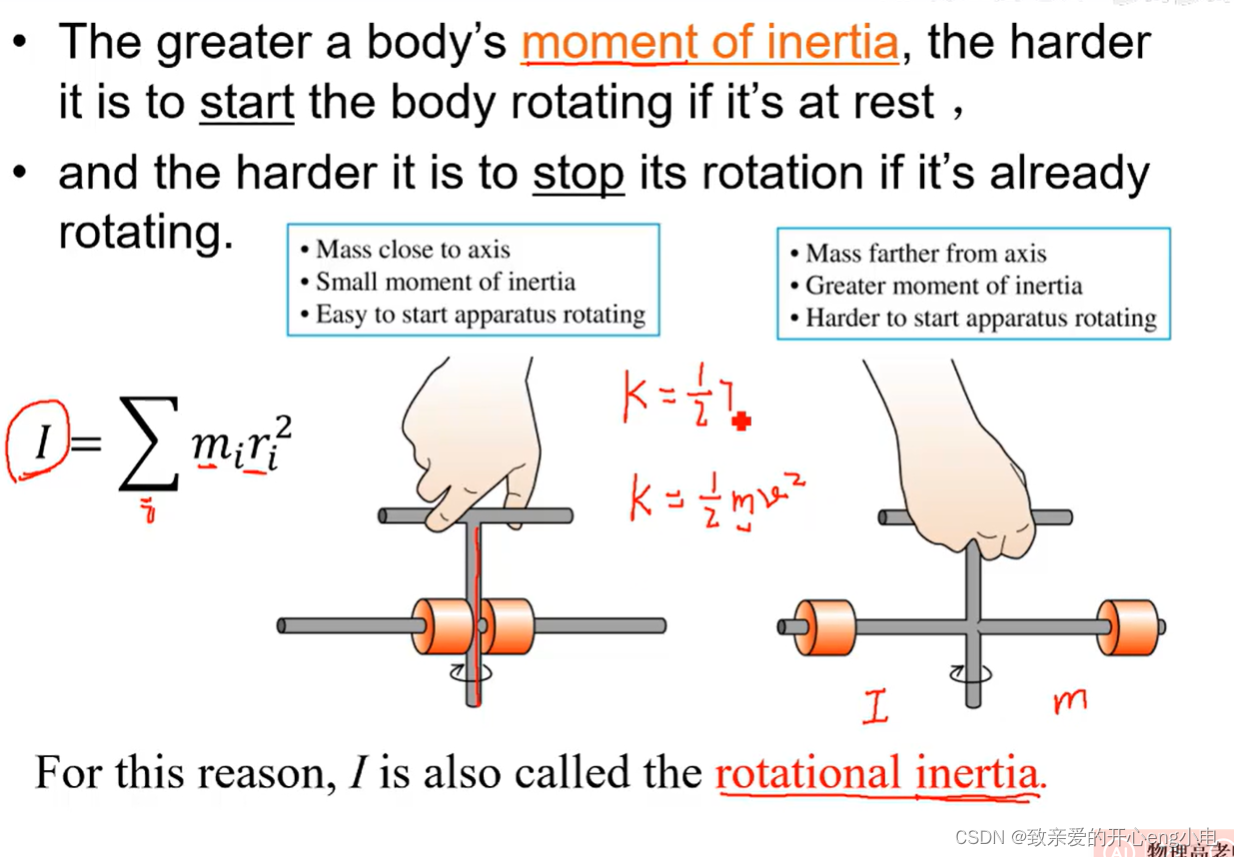
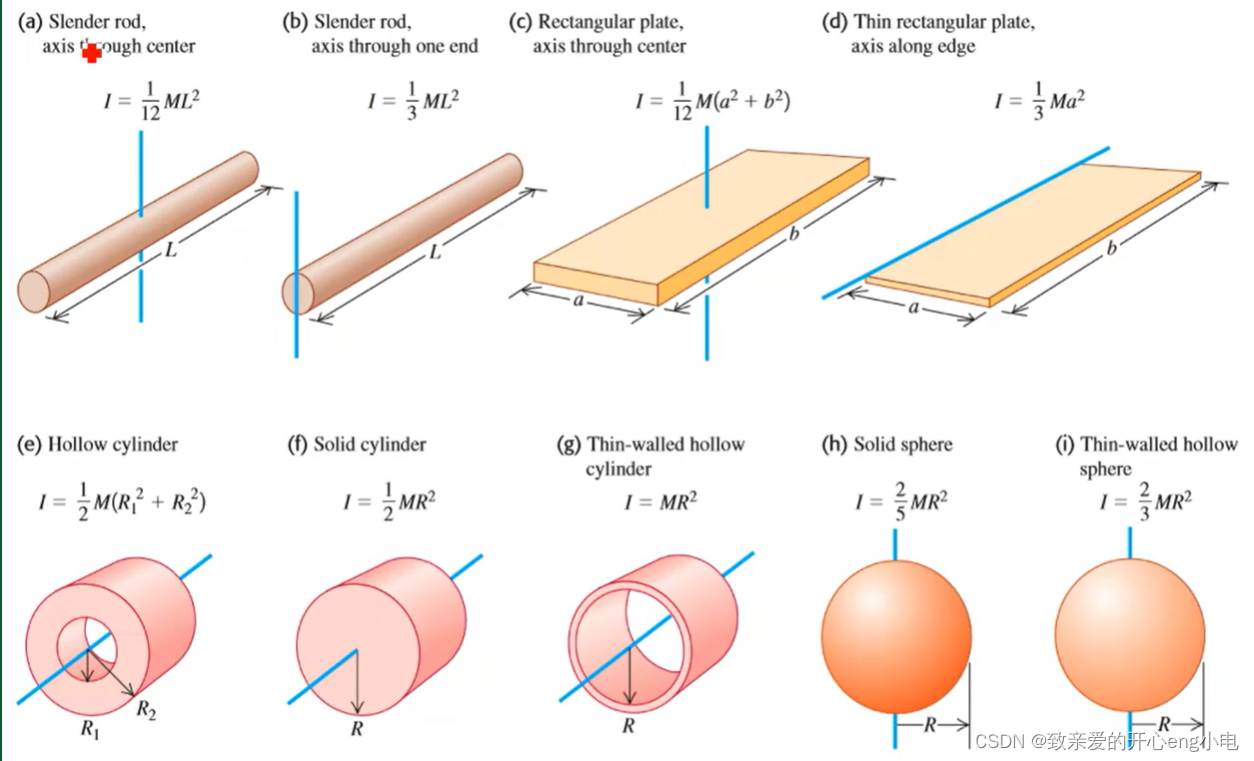
moment of inertia depends on the location and orientation of the axis
](https://img-blog.csdnimg.cn/direct/3f3e0c43e1b54d8db5824bdb6cc6fc9b.gif)